|
經過一段時間的觀察,發現麥田圈現像並不都是零零碎碎的獨立事件,許多麥田圈
相互之間都存在著非常嚴謹的邏輯關系,這看起來就好像在系統地展示一套「啟蒙教
材」。在這裡,將會分幾個部分給大家系統地講解來自麥田圈的信息。這些信息包含了
宇宙萬物的運動生長的基本規律。好吧下面就讓我們來看看這些麥田圈中到底蘊藏了哪
些信息…
第一節:分形(fractal,碎形)
什麼是分形?舉一個最常見的例子:西蘭花

我們可以看到右邊那一小簇是整個花簇的一個分支,而在不同尺度下它們具有自相似的
外形。換句話說,右邊較小的分支通過放大適當的比例後可以得到一個與整體幾乎完全
一致的花簇。因此我們可以說西蘭花簇是一個分形的實例。理解了這一概念讓我們來看
一幅麥田圈。
2002-08-15 United Kingdom

注意到樹頂的那些小圓了嗎? 再看看整體… 整棵被一個大圓容納了起來。清楚了這
點,再結合前面對分形概念的分析,那麼麥圈的含義也就可以理解了。小圓內部結構與
大圓內部結構是自相似的,換句話說,小圓內部不斷重復著大圓內部的結構。 因此可
以用小圓來代替結構自相似的分支,以達到簡化的目的。
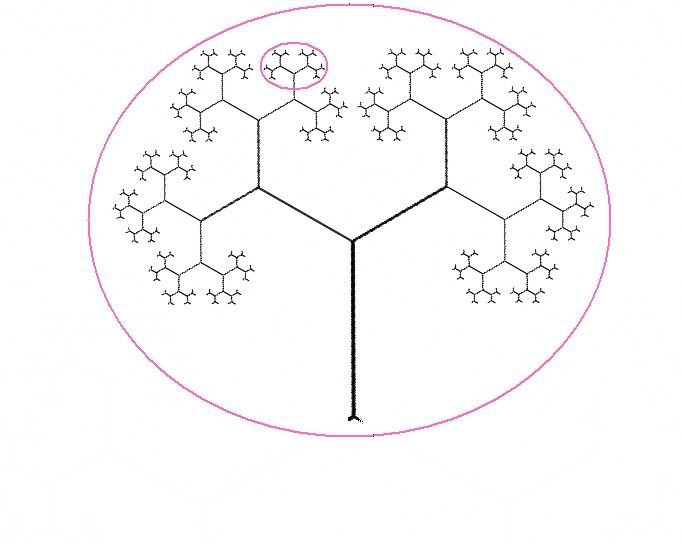
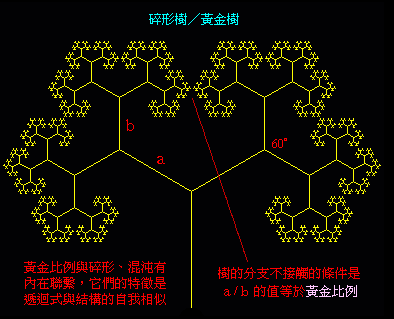
其實,如果你對分形有深入的了解,那麼你應該能輕易看出來,這幅麥圈表達就是「分
形樹」 (fractal tree)的概念,並且麥圈的右半部分符合「黃金比例分形樹」的結
構,如下所示:

除此之外,我們還發現了表示「 門格海棉(Menger sponge)」的分形立體麥田圈圖案。
2009-08-09 United Kingdom

「門格海綿」:

從一個正方體開始。(第一個圖像)
把正方體的每一個面分成9個正方形。這將把正方體分成27個小正方體,像魔方一樣。
把每一面的中間的正方體去掉,把最中心的正方體也去掉,留下20個正方體(第二個圖像)。
把每一個留下的小正方體都重復第1-2個步驟。
把以上的步驟重復無窮多次以後,得到的圖形就是「門格海綿」(Menger sponge)。
注意看上圖第二個立方體,在有光源的情況下,以45度俯視角觀察。便可得到麥田圈所
示立方體明暗分布的圖像了:
 

更多表示「分形」的麥田圈:
曼德布洛特集合(Mandelbrot set)

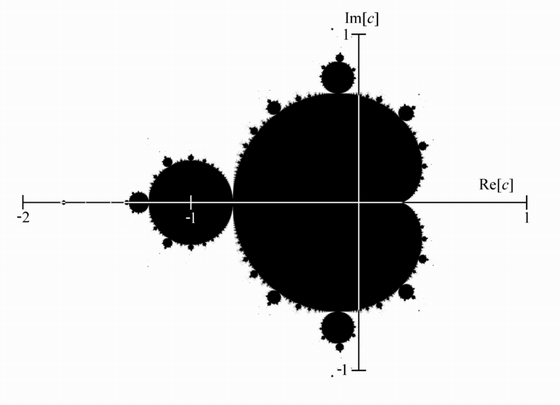

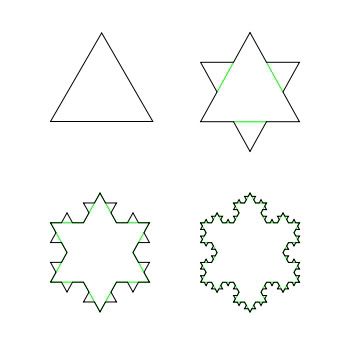
這些來自麥田圈的信息都在提示我們,要用「分形」的思維去理解整個世界,乃至整個宇宙!!
其實,並不單單只有西方文明才有分形的概念。
我們的太極,就是一個最基礎的分形實例:

在一個圓內增加兩個圓,要求這兩個圓相互外切,並且與外圓內切。再經過簡化便得到
了一個最簡單的太極圖。如下圖所示:
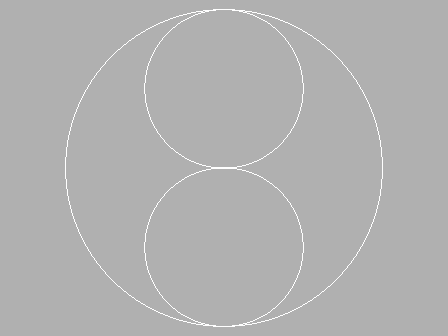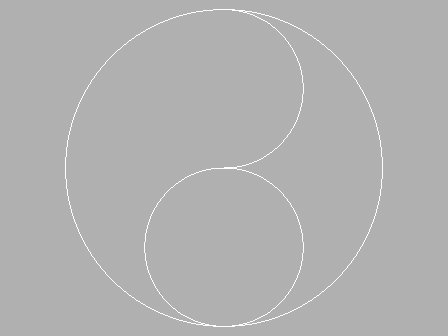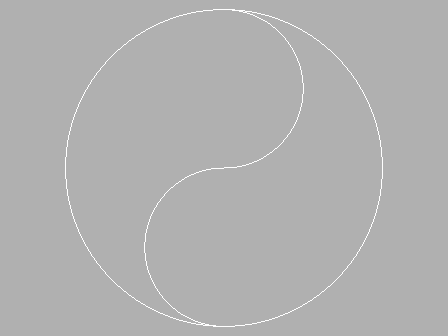
在一個圓內增加兩個圓的過程,稱為:「太極生兩儀」

如果繼續重復「在一個圓內增加兩個圓」的步驟。就形成了下面這幅麥田圈:
2001-07-28 Wiltshire

這一過程就稱為:「太極生兩儀,兩儀生四象,四象生八卦…
受精卵的發育過程同樣依照著這一規律進行,如下圖所示:
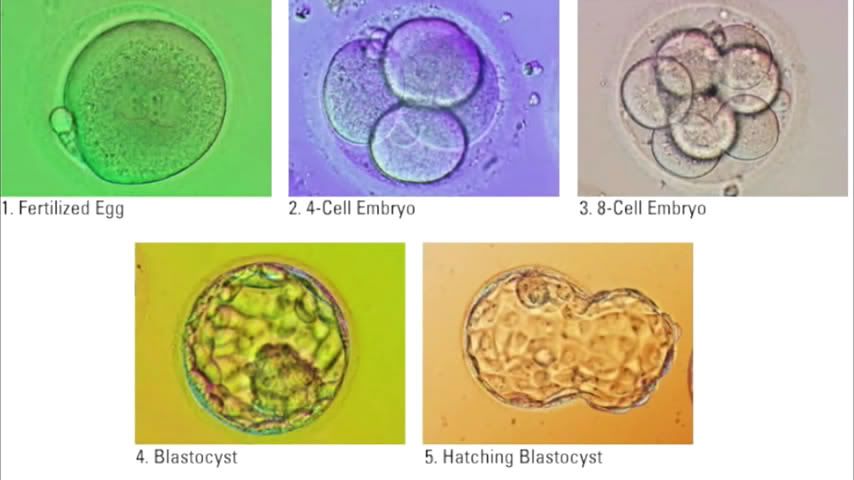
由最初的一個細胞,不斷分裂為兩個,四個,八個… 並且最後發育成胎兒。而人體各
處幾乎都存在分形的實例,比如血管,骨骼間隙。等等… 這些都是由最基礎的分形實
例:太極(受精卵)經過不斷發育分化而形成的。因此具有分形的特征。
分形這部分就先介紹到這裡,通過對這部分的了解,我們知道,「分形」是整個世界,
乃至整個宇宙最為普遍的存在。下一節,將為大家進一步講解麥田圈在植物分枝生長方
面的詳細描述,同時介紹不同麥田圈中相互之間的重要聯系,和它們在各個學科領域內
的重要聯系和啟示。
比如你將會了解到這兩幅看上去毫不相干的麥圈,其實存在著非常重要的聯系!!


附:自然界的分形實例



植物不斷重復特定的生長模式,使得植物各個部分也具有高度自相似的特征。


分形理論:
分形理論在科學領域的應用:
來源:
[ 本帖最後由 taiwanson 於 2010-08-26 07:59 PM 編輯 ] |